| [ TECHNICAL HOME ] | [ RAILROAD HOME ] | ||
|
by Steve Sconfienza, Ph.D. |
D.C. Circuits
Ohm's Law |
- E = I * R
- I = R / E
- R = E / I
- where
- E = Electromotive Force (in Volts); also abbreviated as V
- I = Current (in Amperes); from the French intensité de courant
- R = Resistence (in Ohms)
- Power, in Watts
- = I2R
- = E2/R
Historic Recognition
Electric current
is named after André-Marie Ampère (French), credited with formulating the force law, which he discovered in 1820 (known as "Ampère's Force Law").
Electromotive force
is named after Alessandro Volta (Italian), credited with inventing what was possibly the first chemical battery.
Electrical Resistance
(or something to that effect*)
is named after Georg Simon Ohm (German), who discovered that there is a linear relationship between (1) the potential difference (voltage) applied across a conductor and (2) the resultant electric current: what today is known as Ohm's law.
Power
(electrical or otherwise)
is named after James Watt (Scottish), who was central in the refinement of the steam engine and developed the concept of horsepower.
Also, there are hertz (frequency: Heinrich Rudolf Hertz), farads (capacitance: Michael Farady), henries (inductance: Joseph Henry), coulombs (charge: Charles-Augustin de Coulomb), joules (energy: James Prescott Joule), gauss (magnetic B field [CGS units]: Johann Gauss), tesla (magnetic B field [SI units]: Nikola Tesla), oersted (magnetic H field [CGS units]: Hans Ørsted) weber (magnetic flux [CGI units]: Wilhelm Weber), maxwell (magnetic flux [SI units]: James Clerk Maxwell), more?
* The ohm never measured resistance, per se, but instead the ratio between voltage and current; today, it is related to the "Hall Effect" (discovered by Edwin Hall [American]) the relationship between a voltage induced in a conductive (the Hall voltage) and the magnetic field across and the current through that material (the Ohm is formally defined in terms of the "Quantum Hall Effect"), although the basic concept of the ohm is that which allows one amp through given one volt across (see, for example, in Wikipedia: Ohm, Hall Effect, Quantum Hall Effect [all retrieved May 2014]).
A.C. Circuits
Capacitance |
Capacitive Reactance
- (XC) = 1/(2PiFC) [in Ohms]
- where
- F = Frequency in Hertz
- C = Capacitance in Farads
- If using microfarads instead of farads, the formula is: 1,000,000/(2PiFC)
| µf = 106 | (µf is "microfarads) | (106 is Million) |
| pf = 1012 | (pf is "picofarads) | (109 is Billion) |
| Pi = 3.14159265358979... | ||
Time Constant
- To charge a capacitor to 63.2% of the source voltage.
- or
- To discharge a capacitor to 36.8% of its initial stored charge.
- T = RC
- where
- T = time in seconds,
- R = resistance of circuit in Ohms,
- C = capacitance in farads
- For multiple time constants,
- Two time constants will charge to 86.5% or discharge to 13.5%.
- Five time constants will charge to approximately 99% of source voltage.
- (See the time constant graph under Inductance.)
Energy Stored
- To charge a capacitor to 63.2% of the source voltage.
- En = CE2/2
- Quantity of Charge
- Q = CE
- where
- C = Capacitance in farads
- E = Electromotive Force (in Volts); also abbreviated as V
- En = energy stored joules (wattseconds)
- Q = quantity of charge in coulombs
Above ~10 MHz, capacitors will start acting like tuned circuits due to their inductance [in the leads, etc]: they will block AC and a capacitor of less capacitance will be required to pass higher frequencies.
As the capacitance or frequency increases, the capacitive reactance decreases; as the capacitive reactance decreases, the more AC that will pass, specifically, the higher the frequency of AC that will pass.
Table One A: Capacitive Reactance, 60 Hz - 50 KHz
Power and Audio Frequencies
| Frequency: | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Power | Audio . . . . . . | |||||||||||||
| Capacitance: | 60 Hz | 1000 Hz | 3000 Hz | 5 Khz | 50 KHz | |||||||||
| 100 | µf | 26.53 | 1.59 | XC is less than one ohm | ||||||||||
| 1 | µf | 2,653 | 1.59 | 53 | 32 | 3.2 | ||||||||
| 0.01 | µf | 2.653 105 | 15,920 | 5,300 | 3,183 | 318 | ||||||||
| 100 | pf | 1.591 106 | 5.300 105 | 3.183 105 | 31,318 | |||||||||
| 1 | pf | XC is greater than 2,000,000 ohms | ||||||||||||
Table One B: Capacitive Reactance, 250 KHz to 50 MHz
RF Frequencies
| Frequency: | |||||||
|---|---|---|---|---|---|---|---|
| LF | MF . . . | HF | VHF . . . | ||||
| Capacitance: | 250 KHz | 500 KHz | 1 MHz | 5 MHz | 50 MHz | ||
| 1 | µf | XC is less than one ohm | |||||
| 0.01 | µf | 63 | 32 | 16 | 3.2 | XC is less than one ohm | |
| 100 | pf | 6,264 | 3,183 | 1,591 | 317 | 32 | |
| 1 | pf | 6,264 105 | 3.183 105 | 1.591 105 | 31,830 | 3,183 | |
Table One C: Capacitive Reactance, 100 MHz and above
RF Frequencies
| Frequency: | ||||||
|---|---|---|---|---|---|---|
| VHF . . . | UHF . . . | SHF . . . | ||||
| Capacitance: | 100 MHz | 500 MHz | 1 GHz | 10 GHz | 20 GHz | |
| 100 | pf | 16 | 3.2 | 1.6 | XC is less than one ohm | |
| 1 | pf | 1,591 | 318 | 159 | 1.6 | XC < 1 Ω |
| .01 | pf | 1.591 105 | 31,800 | 15,900 | 159 | 79.5 |
Inductance |
Inductive Reactance
- (XL)= 2PiFL [in Ohms]
- where
- F = Frequency in Hertz
- L = Inductance in Henries
| mL = 103 (mL is "milli-henries") | (103 is Thousand) |
| µL = 106 (µL is "micro-henries") | (106 is Million) |
| Pi = 3.14159265358979 |
Coils
- A single layer, air-core coil of length approximately equal to its diameter approximates the following:
- µL = (r2N2)/(9r + 10l)
- where:
- µL = inductance in micro-henries
r = radius in inches
N = number of turns
l = length of coil in inches - A coil has 1 Henry of inductance for a current change of 1 amp per second, which produces an average counter force of 1 volt within the coil.
Time Constant
- T = L/R
- for current to rise to 63% of its maximum through the coil
- where
- L = inductance of coil in Henries
- R = resistance of coil (or of the L/R circuit) in Ohms
Table Table Two: Time Consant Curve
| RC |
RL |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time Constant t |
% of Change in t |
% of Final Q or V on C when Charging |
% of Initial Q or V on C when Discharging |
% of Final I When Increasing |
% of Initial I When Decreasing |
|||||
| 1 | 63.2 | 63.2 | 36.8 | 63.2 | 36.8 | |||||
| 2 | 23.3 | 86.5 | 13.5 | 86.5 | 13.5 | |||||
| 3 | 8.5 | 95.0 | 5.0 | 95.0 | 5.0 | |||||
| 4 | 3.2 | 98.2 | 1.8 | 98.2 | 1.8 | |||||
| 5 | 1.1 | 99.3 | 0.7 | 99.3 | 0.7 | |||||
Energy
- LI2/2
- (in joules [watt-seconds]) in a coil's magnetic field
- where
- L = inductance of coil in Henries
- I = current through the coil in Amps
Table Three A: Inductive Reactance, 60 Hz to 50 KHz
Power and Audio Frequencies
| Frequency: | ||||||
|---|---|---|---|---|---|---|
| Power | Audio . . . . . . | |||||
| Inductance: | 60 Hz | 1000 Hz | 3000 Hz | 5 Khz | 50 KHz | |
| 30 | L | 11,310 | 188,495 | 565,485 | 942,477 | 9.425 106 |
| 10 | L | 3,770 | 62,831 | 188,493 | 314,159 | 3.142 106 |
| 1 | L | 377 | 6,283 | 18,849 | 31,416 | 314,159 |
| 0.1 | L | 37.7 | 628 | 1,885 | 3,142 | 31,416 |
| 10 | mL | 3.77 | 62.8 | 188 | 314 | 3,142 |
| 3.3 | mL | 1.25 | 20.7 | 62.1 | 104 | 1,037 |
| 1 | mL | 6.28 | 18.8 | 31.4 | 314 | |
| 100 | µL | 1.9 | 3.14 | 31.4 | ||
| 10 | µL | 3.14 | ||||
| 1 | µL | XL is less than one ohm | ||||
Table Three B: Inductive Reactance, 250 KHz to 5 MHz
RF Frequencies
| Frequency: | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| LF | MF . . . | HF | |||||||
| Inductance: | 250 KHz | 500 KHz | 1 MHz | 5 MHz | |||||
| 1 | L | 1,570 106 | XL is greater than 2,000,000 ohms | ||||||
| 0.1 | L | 157,079 | 314,159 | 628,318 | 3.142 106 | ||||
| 10 | mL | 15,708 | 81,416 | 62,831 | 314,159 | ||||
| 3.3 | mL | 5,184 | 10,367 | 20,734 | 103,673 | ||||
| 1 | mL | 1,570 | 3,142 | 6,283 | 31,416 | ||||
| 100 | µL | 157 | 314 | 628 | 3,142 | ||||
| 10 | µL | 15.7 | 31.4 | 62.8 | 314 | ||||
| 1 | µL | 1.57 | 3.14 | 6.28 | 31.4 | ||||
| 0.1 | µL | 3.14 | |||||||
| 0.01 | µL | XL is less than one ohm | |||||||
Table Three C: Inductive Reactance, 50 MHz and over
RF Frequencies
| Frequency: | |||||||
|---|---|---|---|---|---|---|---|
| VHF . . . | UHF . . . | SHF . . . | |||||
| Inductance: | 50 MHz | 100 MHz | 500 MHz | 1 GHz | 10 GHz | 20 GHz | |
| 3.3 | mL | 1.037 106 | XL is greater than 2,000,000 Ohms | ||||
| 1 | mL | 314,159 | 628,318 | ||||
| 100 | µL | 31,416 | 62,831 | 314,159 | 628,318 | ||
| 10 | µL | 3,142 | 6,283 | 31,416 | 62,832 | 628,320 | 1,256,640 |
| 1 | µL | 314 | 628 | 3,142 | 6,283 | 62,832 | 125,664 |
| 0.1 | µL | 31.4 | 62.8 | 314 | 628 | 6,283 | 12,566 |
| 0.01 | µL | 3.14 | 6.28 | 31.4 | 62.8 | 628 | 1,257 |
| 0.001 | µL | XL is less than one ohm | 3.14 | 6.28 | 62.8 | 125.7 | |
IMPEDANCE |
Impedance (Z)
- equals (in Ohms)
- Series:
- Z = (R2 + X2)1/2, where X = XL-XC
- Parallel:
- Y [i.e., 1/Z] = (G2 + B2)1/2, where B = BL-BC
- Definitions:
- X = Reactance, in ohms
- B = Susceptance (B = 1/X), in mhos (mhos = 1/ohms)
- XL = Inductive Reactance
- XC = Capacitive Reactance
- BL = Inductive Susceptance
- BC = Capacitive Susceptance
- G = Conductance, in mhos (G = 1/R)
- Y = Admitance, in mhos (Y = 1/Z)
- Formula Review
- XL = 2PiFL
- XC = 1/(2PiFC) -- or -- 1,000,000/(2PiFC) where C = µf
- BC = 2PiFC
- BL = 1/(2PiFL)
- Vectors
- Xc: V = -j, I = j
- (Voltage lags -- voltage has negative "J Operator")
- Xl: V = j, I = -j
- (Current lags -- current has negative "J Operator")
Figure One, Diagram of Vectors [d]
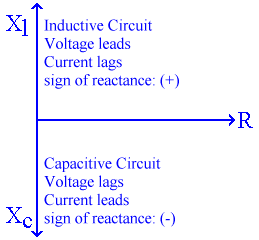
Note that the two formulas for computing impedance,
Z = (R2 + X2)1/2 and Y [1/Z] = (G2 + B2)1/2,
both build a right triangle based on the above diagram, with impedance being the hypoteneuse of the triangle. If the nature of the circuit is of importance (i.e., is it capacitive or inductive), then the direction of the vector can also be indicated based on the sign of the reactance. Note also that this sign is lost when the reactance is squared in computing impedance, as X-squared always has a positive sign.
Parallel circuits with series elements:
- First compute the series impedance in each branch, then . . .
- G (in any branch) = R/Z2
- B (in any branch) = X/Z2
- Y2 =
- (G1 + G2 + G3 + . . . ) +
- (B1 + B2 + B3 + . . . )
RESONANT (TUNED) CIRCUITS |
Tuned circuits are an integral part of inductance, capacatance, and impedance. Applications for resonance and tuned circuits are usually in broadcast and other radio frequency applications (so if you're listening-in you are using a resonant circuit of some sort!).
| The frequency of a tuned circuit equals: | |
| 1/(2Pi * (LC)1/2) = | |
| 0.159/(LC)1/2 or | |
| 0.159/L1/2C1/2 | |
| Q, the figure of merit of the circuit, equals: | |
| of a series circuit = (XL)/R or (XC)/R | |
| of a parallel circuit = R/X | |
| For resonant circuits, | |
| Qp = R/(L/C)1/2 | |
| Qs = (L/C)1/2/R | |
| Using Q, the frequency (F) of a tuned circuit is: | |
| F = (1 - 1/4Q2)1/2/2Pi(LC)1/2 | |
| When L or C are increased, F is decreased; | |
| When L or C are decreased, F is increased. | |
| Half-Power Bandwidth, BW, is related to Q. It is defined as the difference between the upper (f2) and lower (f1) half-power frequencies. It is computed as follows: | |
| BW = Fc/Q | |
| where | |
| BW = Half Power Bandwidth Fc = center frequency of the tuned circuit |
|
Power & Other Electrical Concepts
POWER |
Measuring Power
- Power = I x E
- where
- Power = Watts
- I = Current (in Amps)
- E = Electromotive Force (in Volts; also abbreviated as V)
- alternatively,
- Power = E2/R = I2R
In AC circuits, these relationships are different. AC circuits also have Reactance, the tendency of an inductor or capacitor to resist AC current flow (to DC, an inductor -- a coil -- is a short circuit, while a capacitor is an open circuit). To correct the above DC formulas for AC, the vector of Resistance and Reactance must be computed, which is Impedance (see above). Correcting the DC power formula for AC is done by applying the "power factor."
Power factor:
For parallel circuits:
- IR/IS
-- or --
- G/Y
Note:
- R
- Resistive current or voltage
- S
- Source current or voltage
For series circuits:
- ER/ES
-- or --
- R/Z
For both parallel and series circuits:
- I2R/EA
-- or --
- P/EA
Using cosines:
For parallel circuits:
- cosine [phase angle] = IR/IS
For series circuits:
- cosine [phase angle] = R/Z
In a DC circuit, EA is the power; in an AC circuit, EA is the "Volt-Amperes" (sometimes "VA")
Also, see Impedance (above) for full explanations of G (Conductance, 1/R) and Y (Admittance, 1/Z)
AC/DC Power Relationships:
- DC
- 1 volt DC across 1 ohm = 1 watt
- 1 amp DC through 1 ohm = 1 watt
- AC
For the following,
- Assume that IR = IS (phase angle = 0, power factor = 100%)
- P-P is "Peak-to-Peak," i.e., in one oscillation of the sine wave the voltage measured from the top (positive) peak to the bottom (negative) peak.
- Vrms is "Volts root-mean-square," the effective total voltage under the sine wave.
- 1 volt AC [P-P] across 1 ohm = 0.125 watt:
- 1 volt AC [P-P] =
- 0.5 volt pulsating DC; 0.5 x 0.707 =
- .3535 Vrms
- Power = E x E / R = (.3535 x .3535)/1 = 0.125 watt
- 2 volts AC [P-P], 1 volt pulsating DC, across 1 ohm =
- (.7072)/1 = 0.4949 watt
Using Sines:
An AC voltage, v, can be described mathematically as a function of time by the following equation:
v(t) = A * sin(ωt)
where
- A is the amplitude in volts (also called the peak voltage)
- ω is the angular frequency in radians per second
- t is the time in seconds.
This formula is commonly rewritten as the following:
v(t) = A * sin(2πft)
where
- π is "pi" -- 3.14 . . .
- f is the frequency in hertz
Note the similarity here between this formula (2πft) and the various formulas above:
- 2πfl
- 1/(2πfc)
- 1/(2π * (lc)1/2)
Since, for any angle x, sin(x) can have a maximum value of is +1 and a minimum value is -1, an AC voltage swings between +A and -A. The peak-to-peak voltage, written as VP-P, is therefore
- (+A) - (-A) =
- (+A) + (+A) =
- 2A
AC Motors
- Power Computation
In an AC motor with an essentially reactive circuit (i.e., the impedence is approximately equal to the inductive reactance), the voltamperes may be computed as
E² / Xl
where Xl is the Inductive Reactance (see Inductance above)
So again,
- 1 volt AC [P-P] across 1 ohm = 0.125 voltamperes (VA) . . .
- 1 volt AC [P-P] = 0.5 volt pulsating DC; 0.5 x 0.707 = .3535 Vrms
- VA = E x E / R = (.3535 x .3535)/1 = 0.125 VA
- 2 volts AC [P-P], 1 volt pulsating DC, across 1 ohm =
- (.7072)/1 = 0.4949 VA
But in this purely reactive circuit, with a phase angle of 90%, the power factor is 0, and watts = 0! Changing the motor slightly, if the motor were to have an internal resistance of 2 ohms and a total inductance of 6 milli-henrys (see the table of inductances under Inductance above), and an AC of 60 Hz were applied to it, it would have the following characteristics:
- its inductive reactance at 60 Hz would be approximately 2 ohms
- its impedance (Z=[R² * X²]½) would be
- Z = (2² * 2²)½
- Z = (4 * 4)½
- Z = 16½ = 4 ohms
- its power factor (R/Z, assuming it to be a simple series circuit) would
be .5000 (2 ohms resistance / 4 ohms impedance)
- and its phase angle (not really important here) could be computed as
follows:
- cosine (angle x) = R/Z
- cosine (angle x) = 2/4 = .5000
- .5000 = cosine 60 degrees
Applying 10 volts across this motor would yield 25 voltamperes ((10 * 10)/4)
and 12.5 watts (25 * 0.5), with a current of 2.5 amps.
If an AC voltage of a different frequency were to be applied to the motor, it
would yield the following characteristics:
- it's inductive reactance at 120 Hz would be approximately 4 ohms
- it's impedance (Z=[R² * X²]½) would be
- Z = (2² * 4²)½
- Z = (4 * 16)½
- Z = 64½ = 8 ohms
- its power factor (again assuming it to be a simple series circuit) would
be .2500 (4 ohms R/16 ohms Z)
- and its phase angle could be computed as
- cosine = R/Z
- cosine = 2/8 = .2500
- .2500 = cosine 75.522 degrees
Applying 10 volts across this motor would yield 12.5 voltamperes ((10 *
10)/8) and 3.125 watts (12.5 * 0.25), with a current of 1.25 amps.
Reducing the AC to 30 Hz would be . . .
- Inductive Reactance: 1 ohms
- Impedance: 2.236 ohms
- Power Factor: 0.8945
- Phase Angle: 82.81 degrees
And now 10 volts produces 44.723 voltamperes and 40.004 watts, with a current of 4.4723 amps.
So changing the frequency of the AC has changed the power dramatically. This has a number of consequences. First, changing the frequency (at a constant voltage) will also change key operating characteristics of the motor, such as the power produced and the current flow. Second, since changing the frequency changes the flow of current through the motor, reducing the frequency may result in an unacceptably high current flow causing damage to the motor. Finally, changing the frequency of the AC changes the speed of the rotor.
- Speed Control in AC Motors
To give away the punch-line first . . .
Practically speaking, the
frequency of the AC is how the speed of any given AC motor is controlled. This
is so because of the specific characteristics of AC.
To develop that idea more fully, the speed of any given AC motor is based on the frequency of the applied voltage, the permanent internal construction of the motor, and on the load. Critical in the internal construction of the motor is the number of poles in the stator windings, along with the nature of the wire in the windings and of the component iron (meaning how much current can be applied to the motor and how much of a magnetic field will that current produce). Essentially it is frequency, poles, and load (see AC Motor Speed Table following for how these elements interact).
The load is assumed to be within the ability of the motor to turn. An infinitely large load would be beyond the ability of any motor to turn, while a "too big" load will be beyond the ability of some motor to turn, with the concept of "too big" being based on the motor's internal characteristics: how large is the motor, how much current is it rated for, how much torque does it provide, etc. The ability of the windings to conduct an appropriately high current is necessary for a high-horsepower motor.
Assuming the ability of the motor turn the load (that is, an appropriately rated motor for the load), there will still be some "slip" from the computed speed. The computed speed is called the "synchronous speed," which is when the rotor turns at the same rate as the magnetic field is advancing around the stator. This slip is usually in the area of about 5%, and results in what is called the "full load speed."
By the way, if there were no slip (i.e., if the motor were turning at its synchronous speed, the maximum possible speed for an induction motor), the relative velocity between the stator flux and the rotor motion is zero, thus there is no voltage induced in the rotor windings, hence there is no current flowing in those winding: there is zero torque. Of course, this condition cannot exist for any time under load, slip reappears, and current flows again. This is also the starting problem -- getting the rotor turning, getting slip, getting torque.
Poles are based on the windings of the motor, specifically how the windings are set up inside the motor by their placement and connection, and are in fact the actual magnetic entities of the motors. Since magnetic entities always come in pairs (North & South) [o.k., physics Ph.D.s, show me a real magnetic monopole], the poles of an AC motor also always come in pairs. So a motor may have two poles, four poles, six, eight, and so forth.
The speed of the motor is based on how the AC rotates around the stator, the resulting magnetic field dragging the rotor along with it. The AC energizes the magnetic field in the stator as it passes along the poles. Thus, a formula for computing the synchronous speed of an AC motor is suggested, based on the frequency of the AC and the number of poles. In the real world, the speed of motors is expressed in "revolutions per minute" (rpm) while the frequency of AC is expressed in "cycles per second" (cps or Hz), so a correction of 60 is also required to convert the seconds-based frequency of the AC into the minutes-based speed of the motor. So, since poles always come in pairs, divide the total number of poles by two, then multiply the AC by this number, then multiple by 60 to convert from seconds to minutes. For example, an 18 pole motor at 60Hz would run at . . .
- 18 poles / 2 = 9
- 60 Hz / 9 = 6 6/9ths revolutions per second
- 6 6/9ths rps * 60 = 400 rpm
[Alternatively, if you want to think about it this way, dividing the number of poles into the product of the AC frequency times 120 determines the motor's synchronous speed. For example, as above, for 60 cycle house current that is 60 * 120 = 7,200, 7,200 divided by 18 poles equals 400 rpm. For some reason the formula is sometimes expressed this way.]
In the case above, this same motor, at 120 Hz, would have a synchronous speed of 800 rpm:
- (120 Hz / [(18 poles) / 2]) * 60 seconds = 800 rpm.
Correcting for slip would then mean multiplying this synchronous number by about 0.95, depending on the motor and the load.
This is nice to know: varying the number of poles is a possibility, but in practice it is not widely used, as it is not generally not possible to change the number of poles on the fly. Inherently, the number of poles is typically fixed in an AC motor; however, the stator can be wired so that it can be switched from two poles to four poles to six poles when needed. If the number of poles are doubled, the speed is reduced by one-half, By a special design of the stator windings, leads can be brought out to switch connections that change the number of poles (in the aforementioned two to one ratio: six poles, four poles, two poles). Multiple speeds can be achieved by winding the stator with two or more separate windings. So it is possible, for example, to imagine using transformer taps or a solid-state switch to change the energized segments of the stator, and There are "pole-changing" motors, but that gets very complicated, may require handling huge amounts of current through a solid-state switch, and is genrerally not considered a good idea in very high horsepower applications.
In addition, it is still a rather primative means of control, as it allows for only gross speed changes. A two pole goes twice the speed of a four pole, with nothing in between. If dealing with large numbers of poles, finer speed control may be obtained (24 poles, 26 poles, 28 polse, etc.), but then the synchronous speed of the motor is severely limited ([60*cps]/[poles/2] becomes a very small number when poles is very large). Nevertheless, changing the number of poles is one method of obtaining speed regulation in an induction motor.
Voltage control is obviously an option in controlling any motor. Just like in a DC motor, changing the applied voltage in an AC motor can push more or less electrons through the motor, creating more or less torque to run against the motor's load. So it may seem that one method of controlling the speed of an AC motor is by changing the applied voltage. If the voltage is reduced or increased, the torque produced by the motor is also reduced or increased (and again this is in proportion to the square of the voltage change, the "Vrms" noted above, meaning that a small change in voltage produces a very large change in torque). For most loads, a reduction in driving torque results in a reduction in speed. Varying the applied voltage can, therefore, be considered as a form of speed control for AC induction motors. At low speeds, however, rotor losses become unacceptably high, and it is not possible to achieve stable low-speed, high-torque operation (and this is, after all, the reason not to use a DC traction motor, the intrinsic problems with DC traction at low speeds). So variable voltage as a means of speed control is not normally used with any AC motors. (However, reduced voltage is a strategy for starting AC motors.)
Alternatively, the speed of an AC motor may be controlled by directly controlling the frequency of the applied AC. Since motor speed depends more or less directly on the speed of the rotating field produced by the stator, and this is directly related to the supply frequency, this approach offers many benefits and is the basis of all modern inverter drives (recall that in a modern AC locomotive an inverter changes the DC in the DC link back to AC). Varying the frequency of the AC is not, however, sufficient, for the motor, an inductive electrical load, has a lower impedance with falling frequency, as demonstrated above. With no corrective action taken with regard to the supply voltage, this means the motor current rises as the frequency of the AC is reduced. To compensate for this, the supply voltage must be reduced at the same time as the frequency. By properly reducing the voltage a constant current may be maintained while also maintaining the appropriate torque as the speed is reduced. This process is likewise followed reciprocally as speed is increased.
Using the example of the motor above, and keeping the power developed by the motor constant at 12.5 watts as the speed is changed, yields the following:
- at 30 Hz:
- speed: 200 rpm
- resistance: 1 ohm
- inductive reactance: approximately 1 ohm
- impedance: 2.236 ohms
- phase angle: 82.81 degrees
- power factor: .8945
5.590 volts across this motor yields
13.975 voltamperes ((2.364 * 2.364)/2.236) and
12.5 watts (13.975 * 0.8945), with a current of 2.5 amps. - at 60 Hz:
- speed: 400 rpm
- resistance: 1 ohm
- inductive reactance: approximately 2 ohms
- impedance: 4 ohms
- phase angle: 60 degrees
- power factor: .5
10.00 volts across this motor yields
25.0 voltamperes ((10.0 * 10.0)/4.) and
12.5 watts (25.0 * .5000), with a current of 2.5 amps. - at 120 Hz:
- speed: 800 rpm
- resistance: 1 ohm
- inductive reactance: approximately 4 ohms
- impedance: 8 ohms
- phase angle: 75.522 degrees
- power factor: .2500
20.00 volts across this motor yields
50.0 voltamperes ((20.0 * 20.0)/8.) and
12.5 watts (50.0 * .2500), with a current of 2.5 amps.
Note that the current remains constant while maintaining a constant power (wattage), as the terms in I2R remain constant.
AC Motor Speeds
The following table describes the relationship between some standard AC frequencies and the speed of some standard design AC induction motors. The number of poles in the motor is constant, so the speed is controlled by the frequency of the AC applied. In "normal" circumstances, that is, running an AC motor off 60 cycle AC house current, the speed of the motor will be constant, based solely on the number of poles (and the slippage due to the load); where a variable-speed AC motor is desired some means of frequency control (and therefore also necessarily corresponding voltage control) will be required.
Table Four: AC Motor Speed Table
| Number of Poles |
400 Cycle AC R.P.M. |
100 Cycle AC R.P.M. |
60 Cycle AC R.P.M. |
50 Cycle AC R.P.M. |
40 Cycle AC R.P.M. |
30 Cycle AC R.P.M. |
25 Cycle AC R.P.M. |
|||||||
| Sync. | Full Load |
Sync. | Full Load |
Sync. | Full Load |
Sync. | Full Load |
Sync. | Full Load. |
Sync. | Full Load |
Sync. | Full Load |
|
| 2 | 24,000 | 23,200 | 6000 | 5800 | 3600 | 3500 | 3000 | 2900 | 2400 | 2310 | 1800 | 1750 | 1500 | 1450 |
| 4 | 12,000 | 11,600 | 3000 | 2900 | 1800 | 1770 | 1500 | 1450 | 1200 | 1150 | 900 | 860 | 750 | 720 |
| 6 | 8000 | 7680 | 2000 | 1920 | 1200 | 1170 | 1000 | 960 | 800 | 770 | 600 | 575 | 500 | 480 |
| 8 | 6000 | 5800 | 1500 | 1450 | 900 | 870 | 750 | 720 | 600 | 575 | 450 | 375 | 375 | 360 |
| 10 | 4800 | 4600 | 1200 | 1150 | 720 | 690 | 600 | 575 | 480 | 460 | 360 | 340 | 300 | 285 |
| 12 | 4000 | 3840 | 1000 | 960 | 600 | 575 | 500 | 480 | 400 | 385 | 300 | 285 | 250 | 240 |
| 14 | 3424 | 3280 | 856 | 820 | 514 | 490 | 428 | 410 | 343 | 330 | 257 | 247 | 215 | 205 |
| 16 | 3000 | 2880 | 750 | 720 | 450 | 430 | 375 | 360 | 300 | 288 | 225 | 215 | 187 | 180 |
| 18 | 2664 | 2542 | 666 | 638 | 400 | 380 | 333 | 319 | 266 | 256 | 200 | 190 | 167 | 160 |
| 20 | 2400 | 2280 | 600 | 570 | 360 | 340 | 300 | 285 | 240 | 230 | 180 | 170 | 150 | 143 |
| 22 | 2224 | 2080 | 546 | 520 | 326 | 310 | 273 | 260 | 218 | 208 | 163 | 155 | 138 | 130 |
| 24 | 2000 | 1920 | 500 | 460 | 300 | 285 | 250 | 240 | 200 | 192 | 150 | 143 | 120 | 115 |
| 30 | 1600 | 1552 | 400 | 388 | 240 | 230 | 200 | 192 | 160 | 153 | 120 | 115 | 100 | 96 |
Magnetic saturation
This is a rather abstract concept that may best be thought of as the limited ability of an object to be magnetized. In the case of a motor the object is usually a piece of iron wound with wires conducting an electrical current.
A coil of wire is an inductor, that is a magnetic field may be induced within the coil (see inductors above). When a voltage is applied to the wound wires in the motor (the coils or inductors), a current is caused to flow, and that current flow causes a magnetic field to be created. With more applied voltage, more current flows and there is more of a magnetic field in proportion to the applied voltage. This is a linear relationship.
At some point, the iron becomes saturated: that is, increasing the current does not create more magnetic field, and the linear relationship is broken: increasing voltage no longer causes a linear increase in current but instead creates a geometric increase in current -- that is, lots and lots of current, creating lots and lots of heat, burning out the motor.
This may best be thought of in terms of a graph. The graph of a magnetic field can be thought of as starting at the origin (0,0) and increasing/decreasing linearly from there (in opposite directons) as the magnetic field magnetizes the iron of the core, ultimately reaching a point (in either direction) where the effect levels.
Figure Two, Magneic Saturation
Applied Voltage / Magnetic Field Strength [d]
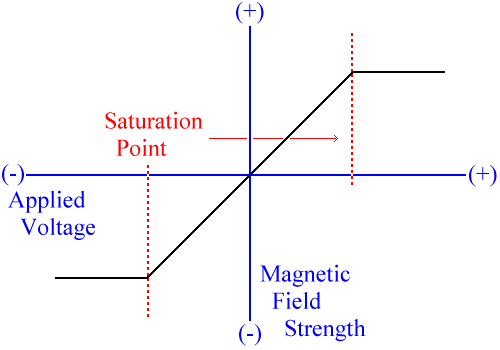
Any motor (AC or DC) is an electro-magnet. When voltage to the motor, thus to the electro-magnet, is increased, current increases in direct proportion (I=V/R), but this only works (in the electro-magnet) up to a point. After that point current increases exponentially. That is, because the iron core or any material (in the real world of working motors) can only conduct a limited amount of magnetic flux, once that point is reached current will have the tendency to become very high with a very small increase in voltage. This is called magnetic saturation and is sometimes seen in motor applications. Correspondingly, current can drop from that very high level with a small adjustment of voltage down, but this is too dangerous an area of operation for that principal to be of any operational use: the point is to avoid this point. The point is actually to operate the motor as close to saturation as possible, but not to go let it go into saturation.
Figure Three, Magnetic Saturation
Applied Voltage / Current Flow [d]
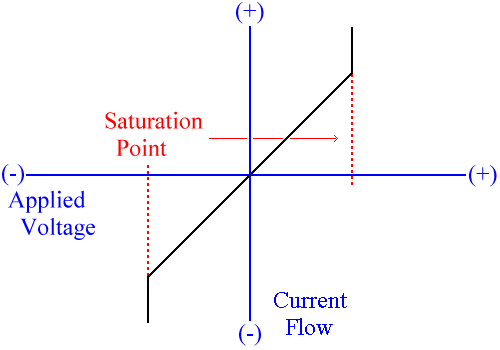
Figure Two is also the basic, s-shaped, B-H curve, the graph of
- B, the magnetic flux density, expressed in units of gauss (generally measured in milligauss), which is the total magnetic effect that results from the applied force, and
- H, the magnetic field, expressed in units of amperes per meter (A/m), which is the the magnitude of the magnetic field vector, i.e., tendendcy to magnetize space.
The actual slope of the curve, u, in the region of the origin (0,0) is expressed by the formula
- u = u0ur
- where
- u0 is the permeability of free space, and
- ur is the relative permeability of the material.
B and H are approximately linked with the simple equation
- B = H * u
This results in the aforementioned s-shaped curve that crosses the origin linearly (slope of 1/1 or some such, whatever the above equation yields) and flattens on the ends (to a slope of 0/1).
Eventually, all the magnetic domains align with the applied field, and the curve flattens out as the iron core becomes magnetically saturated. As the applied magnetic field is reversed, the iron eventually becomes magnetized in the reverse direction until it again saturates. When saturated, the application of an increased voltage will not be attenuated (in part) by the work spent magnetizing: rather, current will increase dramatically. Motors may burn-out in a matter of seconds in this state.
Electric Power Transmission |
When utilizing a power system where the underlying power itself is remotely produced, that is, when utilizing a central generating plant to produce power consumed in remote locations, the means of transport for the power, between the generation site and the consumers, is of critical importance. The quality of the electrical supply to the users, in the case of electric railroads the users being the electric locomotive or MU power cars, is essentially the quality of the voltage provided. While power is derived from the flow of electrons (the flow of electrons -- the current flow -- as measured in amps) through a circuit (in the case of moving a train, the current flow through electric motors), it is the maintenance of a constant voltage that is critical to the uninterrupted and stable delivery of current.
Many factors influence the quality of the voltage delivered. These include those intrinsic in the infrastructure (transmission lines) as well as the results of power consumption itself. Problems may be manifested by short- or long-term periods of variation from the normal voltage, along with rapid voltage changes, deviations, dips (or sags -- "brown-outs"), fluctuations and flicker, or unbalance of 3-phase voltages (i.e., different voltages among the phases in a three phase system). In addition, there may occur other irregularities, which may include variations in frequency and the presence of non-linear system or load impedances that will distort the voltage waveform, along with transient spikes and surges that may be propagated along circuits in a supply system. In an ideal AC power system, the voltage and frequency at every supply point would be constant and free from harmonics, and the power factor would be one. Various approaches are used to mitigate these problems. One of the most critical areas to be addressed is the stablity of the transmission system.
The Transport of Large Amounts of Electrical Power over Long Distances:
High-Voltage Transmission Lines
In rail applications (as in most others), the most efficient transmission of electricity from generating stations to the tracks requires transmission lines of high-voltage. In the United States this is done (almost universally) with AC transmission lines and with substations to convert this to line voltage for local use.
Electric transmission lines criss-cross the United States, with their characteristic sets of three wires (or goupings of three wires). Each of the three wires (or wire groups) is one phase of a three-phase AC set. There are also characteristically ground wires above or below the transmission wires. This is the standard long distance, high voltage transmission line in the United States. In fact, AC transmission is so ubiquitious that the possibility of using DC is sometimes forgotten; however, in certain long distance applications, DC may be more economical than AC.
The transmission of large amounts of electrical power over long distances is is done with high-voltage lines. High-voltage lines are used because the line losses are much smaller than with low-voltage lines.
All wires currently used have some internal resistance (the development of high-temperature superconductors suitable for long-distance transport would change). The total resistance of the transmission line leading from a power station to the local substation may be called R. The demands of the local conusmer for power from that substation may be expressed in the formula
P=IV
where P is power, I is current, and V is voltage (we're going to use V here for "voltage" instead of E for "electromotive force" as we want to stay focused on the concept of voltage in the power lines). This means the current drawn by the substation (rearranging algabraicly) is
I=P/V
Current and voltage have an inverse relationship, so the higher the transmission line voltage, the smaller the current.
The line loss (that is, the power consumed in the line) may be expressed by the formula
Ploss=I2R
Note: the formula above and all those following assume a phase angle of zero, which in fact is what one strives for in transmission lines.
Doing some substitution (for I, V/R; for R, V/I; for P, V2/R),
- divide both sides of the equation by power through the line,
Ploss / P = I2R / P
- on the right side of the equal sign, substitute for the R in the numerator and for P in the denominator,
Ploss / P = ( I2*[V/I] ) / ( V2/R )
- which simplifies to
Ploss/P = ( I * V ) / ( V2/R )
- which rearranges to
Ploss/P = ( I * V ) * (R / V2)
- which simplifies (finally) to
Ploss/P = ( P ) * (R / V2)
- so
Ploss/P = PR/V2
The fraction Ploss/P is the percentage loss in the line, or the "loss fraction."
Since P is fixed by community demand (as it exists at any given time), and R is as small as can be made (using heavy copper cable, for example) and generally fixed; thus,
- holding R constant, the right side of formula six reduces to
Ploss/P = P/V2
Line loss decreases dramatically with increasing voltage, decreasing logarithmicly, as the voltage -- in the denominator -- is raised to the second power. Of course, voltage is another design aspect of the system: it cannot be raised on the fly, so the point is to design the system with the highest practicable voltage.
Another important note: the loss fraction (what was computed above, formula 7) increases with increasing load P: power transmission is less efficient at times of higher demand. As P -- in the numerator on the right side of the equal sign -- is at the first power, the loss fraction increases linearly with increasing power demand. Again, this is because power is proportional to current but line loss is proportional to current squared (see formula one above).
Keep in mind that what is happening is that as power demand increases, and voltage is fixed by the characteristic design of the transmission line, the current increases linearly with power demand [P=I*V]; so,
- formula 7 cross-multiplies to
Ploss * V2 = P2
and, given that V is constant in any given power line (within the working load conditions of the system, including—ultimately—the source generating capicity),
- formula 8 becomes
C * Ploss = P2
and again it is evident that power loss is a logarithmic function, and power loss is minimized by keeping C [i.e., the line voltage] as large as possible.
Line loss can be quite large over long distances, up to 30% or so. By the way, line loss power goes into heating the transmission line cable which, per meter length, is not very much heat, but may be enough to make the cable sag: under extreme loads, it may be sufficient for the cable to sag enough to contact objects underneath the transmission lines, causing direct shorts to ground (and failure of the transmission system).
So the point of all of the foregoing is that it is best to use the smallest amount of current that can deliver the power being demanded, this done by designing a system for transmission with the highest voltage possible given the economic circumstances. When current through the system gets "too large" -- whatever the circumstances allow "too large" to be defined as -- it is time to build a new transmission line: one option would be to build a new line of like characteristics if the original line is to be retained; a second option would be to build a new line with a substantively higher voltage level as an outright replacement (e.g., replacing a 345 kV line with a 765 kV line).
Formula Note:
A note on formula 9 above, the premis being that V is constant and thus becomes a constant in the formula: that premis fails when the load exceeds the ability of the system to maintain the supply:
- In effect, more current is demanded than the system can deliver.
- This presupposes that the system is originally built with the ability to supply more current at busy times and less current at less busy times: at some point, that busy-times reserve may be exhausted.
- When that happens, the current level plateaus, and as total load increases beyond that point
the voltage drop across any resource on the system begins to fall; i.e.,
- imagine this as a simple parallel circuit having voltage drops in each leg of the circuit identical to the source voltage;
- assume this source to be a regulated voltage:
- as load increases to, through, and beyond the ability of the regulator to maintain the constant voltage, the overall voltage across the source drops.
Individuals customers would see this as a decrease in the current delivered at any single resource. With the voltage drop occuring in each leg of the circuit, the current through the loads drop as well: this is the "brown-out" scenario:
- Given that
- total current in the system has plateaued at its maximum level and is now constant
- the voltage regulated system has become, effectively, a current regulated system
- adding additional (parallel) load reduces the current in each leg,
- thus the voltage drop across each leg drops as well
- total current in the system has plateaued at its maximum level and is now constant
- At any given load,
- with a total load in excess of the system capacity,
- as current through the given load drops the voltage will tend to stabilize at a lower level
- Re-arranging Ohm's law demonstrates this: e.g.,
- holding I constant in a parallel circuit,
- increasing R (i.e., the load) in an individual leg, or adding an additional leg with no corresponding reduction otherwise in laod, lowers R overall in the system,
- thus, overall, with I=V/R, as overall R decreases, so does V.
- holding I constant in a parallel circuit,
Alternating Current versus Direct Current
Note that the above formulas treat the transmission medium as a purely resistive load to the AC: that is, at 60Hz, a straight wire has essentially zero inductance (thus no inductive reactance). The medium has high, but not infinite, capacitance, and the parallel wires act as a shunt capacitor (i.e., a capacitor across the load): thus it does have capacitive reactance. The loads on power lines are almost all inductive (motors, light bulbs, toasters), so there is a tendency (one thinks; one hopes) for the inductive reactance of the loads and capacitive reactance of the transmission lines to cancel each other. In practice, at any given time, the total system may be capacitive or inductive, (current may be leading or lagging); therefore, it is generally close to, but not completely, a purely resistive load (there is some phase angle, preferably not much, and in practice the line is most efficient when phase angle is zero).
There may be significant radiation with the transmission lines acting as antennas. At a frequency of 60 Hz, the wavelength of the AC is about 3,100 miles.
γ=V/ƒ
where γ is wavelength, V is velocity, and ƒ is frequency.
γ=[300,000,000 meters/second]/[60 cycles/second]
γ=5,000,000 meters/cycle
(That is, one wave is 5,000 kilometers, or 3,100 miles, long.)
These long lines are frequently in the range of quarter waves (1250 kilometers, 775 miles). These would be long enough for considerable radiation.
There are numerous examples of long distance, high voltage transmission lines that use DC. These are generally what are called a bipole system, referring to a positive (+) and a negative (-) pole across an earth ground (not unlike the grounded neutral in +/0/- AC systems), thus generally indicated as +/- V. Transmission is possible over many hundreds of miles, far greater distances, theoretically, than AC, which has practical limits of around 750 miles (1200 kilometers).
The principle of high voltage DC transmission is simply converter stations on each end of a transmission line: at the source there is one converter station housing the rectifier system (AC to DC), then there is a transmission line, and at the destination a second converter station housing the inverter system (DC to AC). (Generation and distribution are still accomplished in AC, generation because AC machinery is less complex and less costly to maintain [no brushes], and distribution because it is easier to step down voltages at various stages in the local system.) The rectifier is a standard 3-phase AC rectifier that gives the +/- voltages. (It can be single, +V voltage, but it is generally more simple to use two half voltage lines than one full, which is (again) similar in principal to the three-wire residential service most homes in the United States have.) The transmission line has two or three wires in the -V,0,+V voltage system (with the grounded neutral).
A leader in energy transmission via DC lines is Russia: they have air-lines running +/-750 kV that are several thousands kilometers long. Manitoba Hydro (in Canada) has two bipole lines in their Nelson River DC Transmission System, one +/-450 kV, the second +/- 500 kV, each approximately 900 kilometers long (running to just northwest of Winnipeg). In the United States, Minnesota Power (now called Allete) is using DC from a power plant at the mouth of a coal mine in Montana that sends very high voltage to Duluth. The Duluth line runs two wires and ground (two wire is 95% efficient, and if one wire is out, they can run one wire and ground at 92% efficiency). The station ground is located some distance from the plant, and reportedly consists of huge pits filled wth salt.
In DC transmission (as in any DC applications), the inductance and capacitance of the conductor have no negative effects, as there are no inductive or capacitive effects, thus no inductive or capacitive losses. The electrical field in a DC cable is generally evenly disposed, especially in round cables. Corona effects (ionization of the air around the transmission wires) are similar to, although not identical to, AC. Underwater DC cables are also specifically different than AC cables. In submarine lines, water all around the cable gives a shielding effect, so the voltage applied to the DC cable can be considerably higher than the voltage in an AC cable.
With respect to the transmission of high quantities of electrical energy over long distances as the only criteria, DC transmission is effective because DC lines are less expensive than AC (typically two wire instead of three) and DC has considerably less losses (no reactive - - specifically capacitive - - losses and no radiation with long air lines): some estimates put DC at about 30% more efficient than AC. Other issues at the super-high voltage levels such as corona are as much or more pronounced with AC than DC. In the case of underwater transmission there is the additional reason of DC cables being able to support very high voltages and transmit a correspondingly higher energy than AC cables. These cables have less energy losses and the price of the cables is less than the AC equivalent. For these reasons, a DC cable can generally have less copper than AC cable, thus the transmission medium itself can be less expensive than in AC systems.
With all of its advantages, DC has at least one critical flaw: high voltage conversion is an issue. Modern inverters (the DC to AC converter) are generally thyristor based: they have a large number of ultrafast thyristors connected in serial. These are very efficient, but are a very expensive part of DC transmission; likewise, solid state rectifiers are very efficient but very expensive. These elements of the infrastructure simply do not exist with AC transmission systems. Further, progressively stepping down the voltage in the local distribution network confronts the same issues of size and expense: it is an expensive proposition to reduce a high DC voltage to a lower DC voltage
With AC, stepping down the voltage in the distribution system may be done on the fly, so to speak. It is a simple matter to reduce a high AC voltage to a lower AC voltage using step-down transformers (these may be seen at substations and on power-poles). A step-down transformer reduces voltage and increases current so that the power (voltage * current) is constant (and, ideally, loss-less, or as near so a technically possible). A neighborhood substation typically reduces the voltage to a reasonable value for street lines, say 13.8kV, and then a small transformer on the pole reduces it to +/- 110 volts (220 volts in Europe) (see more on substations under Electric Locomotives on the Locomotive Information page). (The alternation frequency is 60 cycles/sec [60 Hz] in the US [50 cycles/sec (50 Hz) in Europe].)
The choice between AC and DC is central to the effort to reduce line loss by using high voltage. For the reasons enumerated above, in DC transmission systems conversions at both ends of the transmission line are necessary, making short-distance DC transmission not cost-effective. However, when very long distances are involved, greater than about 750 miles (1200 killometers) AC may be impracticable, while DC would become quite cost-effective.
So, overall, DC transmission systems are not used as standard systems in the United States for economic reasons as much as for technological reasons; in fact, they present technological advantages, but in electric systems with numerous, relatively local generating facilities, the costs of the converter stations outweigh the economies of the transmission. What we see here in the U.S., serving our communities and along our railroad rights-of-way, is AC.
AC Frequency Usage
Various frequencies are in common use. Northeast railfans know 25 hertz as the frequency for the Pennsylvania Railroad's mainline electrification. However, it is generally accepted that Nikola Tesla chose 60 hertz as the his standard for power distribution as it was the lowest frequency that would not cause street lighting to flicker visibly and it had efficiencies in transmission over lower frequencies, and is an efficient multiple of the time base (of 60). The origin of the 50 hertz frequency used in other parts of the world is generally conceeded as a concession to the metric system, although this frequency may have significantly higher line losses than 60 hertz, with losses in some applications greater than 60 hertz in the 10% to 15% range.
Other frequencies were common in industrial use in the first half of the 20th century, and some remain in use: 25 Hz AC (much of it generated at Niagara Falls), was used in Ontario and the northern USA. Some 25 Hz generators were in use at Niagara Falls up until the mid-1990's for large industrial customers who did not want to replace existing equipment.
The lower frequency eases the design of low speed electric motors, especially commutator-type motors for electric traction applications such as railways (e.g., the commutator-based AC motor in the GG1), but would cause a noticeable flicker if used in lighting. Along this line, 16.67 Hertz (which multiples times-3 to 50.0) is used in some European rail systems (e.g., Sweden).
Some aircraft, spacecraft, computer mainframe, off-shore, marine, and textile industry applications use 400Hz. This is for the benefits of the reduced weight of apparatus or the higher motor speeds obtainable in synchronous motors.
References:
- Global Enerty Network Institute, Newsletter, Winter-Spring 1992
- Global Enerty Network Institute, Electrical Transmission
- Nautilus Institute, Basic Principles Of Interstate Electrical Power Links . . .
- Manitoba Hydro
- Wikipedia, Alternating Current
- School for Champions, Worldwide AC Voltages and Frequencies
# # #
| revised 5 February 2015 | Go to Railroad home page | [ TOP ] |